We know that the airplane lift coeffecient varies inversely with the square of the air speed:
CL = (W/S)/(0.5*rho*V^2), - eqn. 1
where,
CL is the airplane lift coeffecient, approximately equal
to the wing lift coeffecient,
W/S is the wing loading = (airplane weight/wing area),
rho is the air density, and
V is the flight speed
We also know that for a given chord, Re varies linearly with flight speed:
Re = rho*V*c/mu, - eqn 2
where,
Re is the Reynolds number at any section whose chord is c, and
mu is the dynamic viscosity of air
We can see from eqn. 2 that the Reynolds number changes as we increase speed from stall speed to cruise speed. So if we want to examine airfoil data, we have to look at stall characteristics at the Re corresponding to stall speeds, the climb performance at Re for climb and cruise perofrmance for Re corresponding to cruise speeds.
To avoid having to look at curves for different Re for different flight conditions, we can instead use reduced Re. From eqn.1 and eqn. 2, we can see that
Reduced Re = Re*sqrt(CL) = (1/mu)*sqrt(2*(W/S)*rho)*c - eqn 3
From equation 3, for a given atmospheric condition (say sea-level) , wing loading, and chord, the reduced Re is a constant, even though the actual Re changes with flight speed.
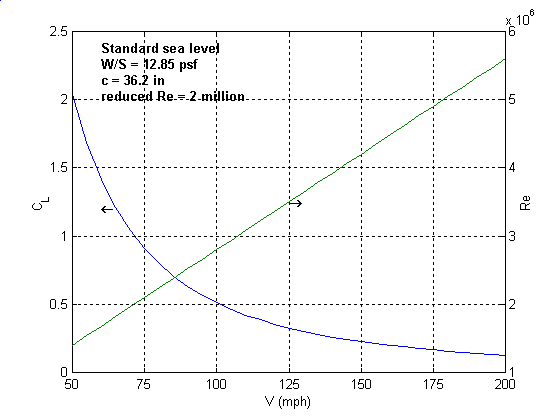
The following figure shows the variation of CL and Re for a W/S of 12.85 psf, a chord of 36.2 inches and a reduced Re of 2 million at sea level. As seen from the figure, even though the actual Re varies with flight speed from about 1 million to about 6 million, the reduced Re is always 2 million.
